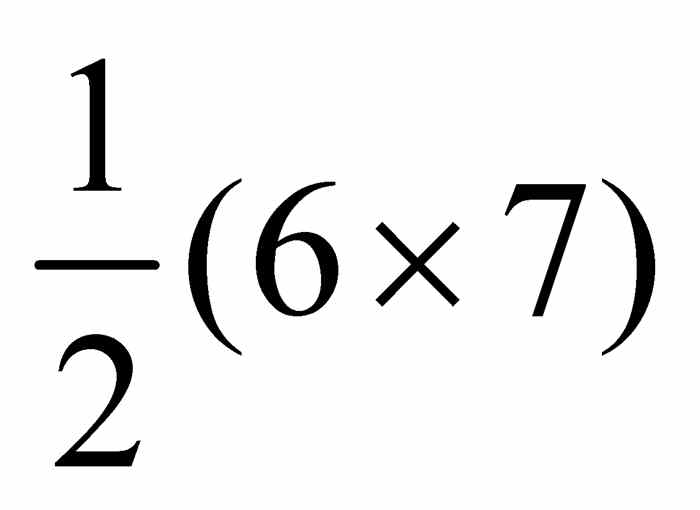 .用同样的方法,对任意正整数n,有
.用同样的方法,对任意正整数n,有 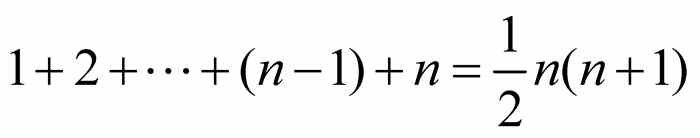
下面的问题与文中讨论的内容有关.你可以通过这些题目思考并熟练掌握一些基础数学知识.
问题1 考虑图1-10(a)中的图形.自顶而下点的总数是1 + 2 + 3 + 4 + 5 + 6.而 图1-10(b)中点的个数为
2(1 + 2 + 3 + 4 + 5 + 6) = (1 + 6) + (2 + 5) + (3 + 4) + (4 + 3) + (5 + 2) + (6 + 1) = 6 × 7
因此1 + 2 + 3 + 4 + 5 + 6= 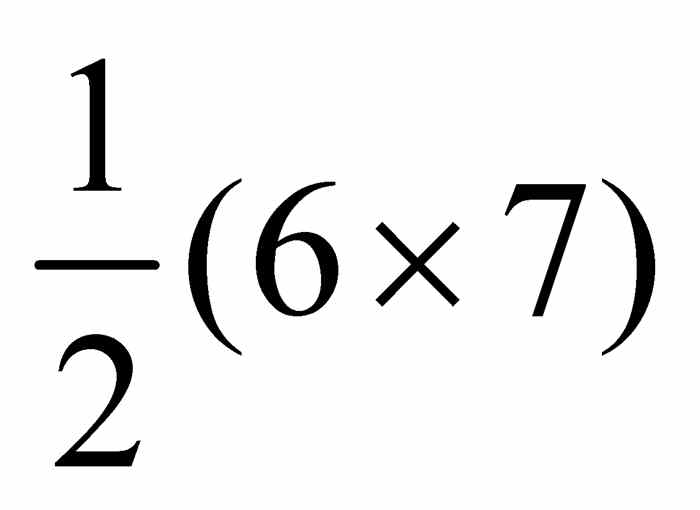 .用同样的方法,对任意正整数n,有
.用同样的方法,对任意正整数n,有 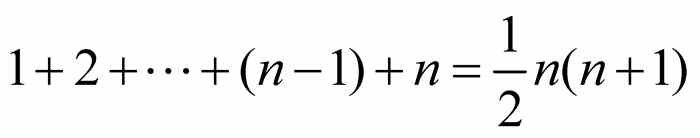
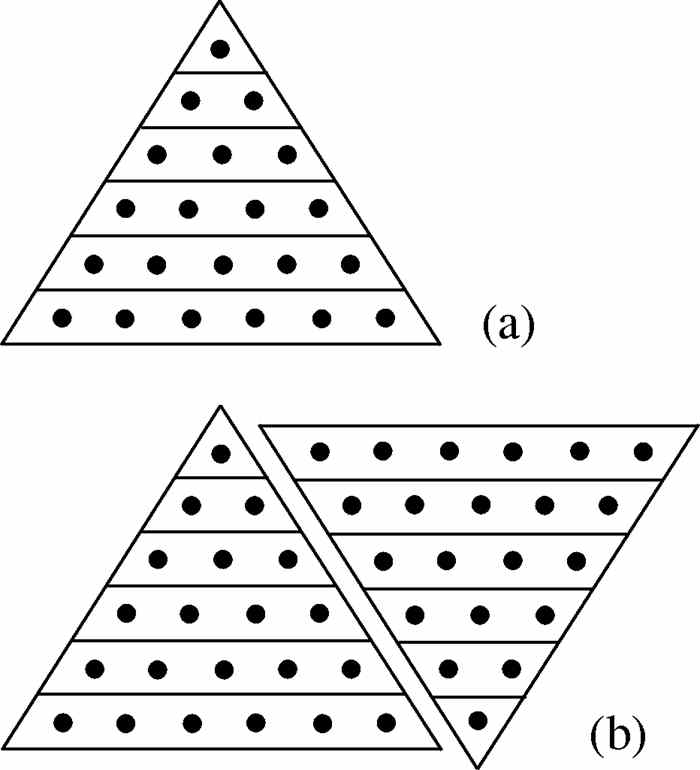
图 1-10
问题2 从1开始的任何连续奇数的和应该都是平方数,例如1 + 3 = 22、1 + 3 + 5 = 32、1 + 3 + 5 + 7 = 42、1 + 3 + 5 + 7 + 9 = 52 .图1-11表明1+3 +5 +7 +9 + 11=62 .假设n为任意正整数,考虑奇数2 k-1.令式中的 k = 1,k = 2,…,k = n,则前n个奇数列为1, 3, 5, … ,2 n-1.证明它们的和1 + 3 + 5 + … + (2 n-1)等于n2.【提示:用与问题1相同的求解方法可得.】
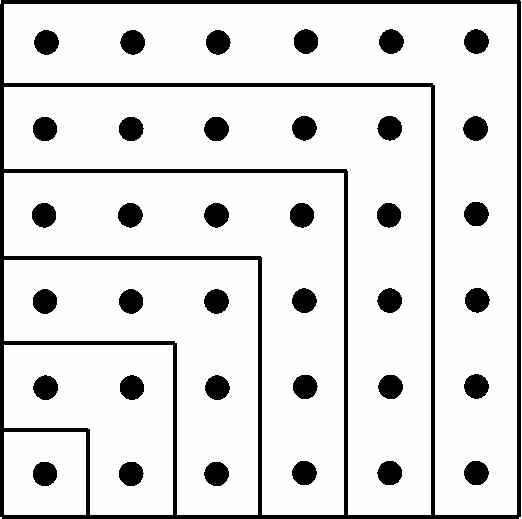
图 1-11
问题3 取任意两个正整数m和n,n>m.令 a = n2 - m2 、 b = 2 nm 、 c = n2 + m2,可得到正整数a,b,c.这便是生成能满足 a2 + b2 = c2 的数a,b,c的方法.取m=1,n=2,可得a = 4-1 = 3, b = 2×2 = 4, c = 4 + 1 = 5.因为32 + 42= 52 ,可见在这个例子中这种方法有效.取m=2,n=3,可得a = 9-4 = 5, b = 2×6 = 12, c = 9 + 4 = 13.因为52+ 122= 169=132 ,同样,在本例中这种方法也有效.证明一般情况下这种方法成立,并用它列出其他5组满足 a2 + b2 = c2 的正整数(a, b, c).
问题4 研究图1-12所示的三个图形.直角三角形边长为a、b、c,其中c已给定.中间的图有两个正方形,这两个正方形按照如下方式安排,即它们所确定的4个三角形区域均与给定的三角形全等.利用这些图,写出验证毕达哥拉斯定理的过程.
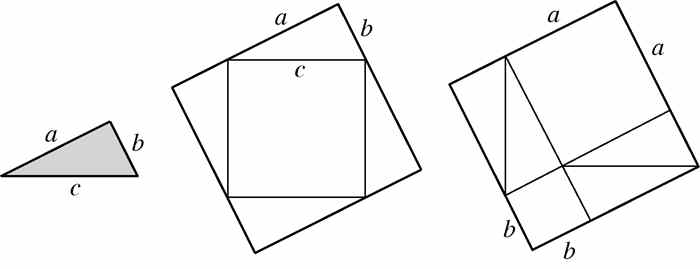
图 1-12
问题5 中国人也知道毕达哥拉斯定理.用图1-13(b)表示图1-13(a)的中国古代图形的基本信息.它在一个正方形内绘制了4个相同的直角三角形(每个的边长均为a、b、c).确定里面正方形的大小,并用该图来验证毕达哥拉斯定理.
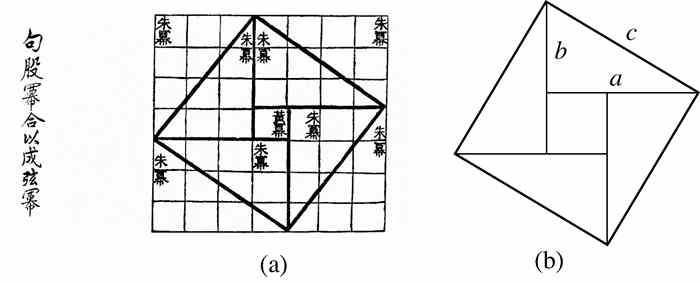
图1-13 (a) 是中国的勾股定理,选自《中国科学与文明》(Science and Civilization in China)第3卷:《天和地的数学与科学》(Mathematics and the Sciences of the Heavens and Earth),李约瑟(Joseph Needham)著,台北敦煌书局出版,1986,p22
讨论1.1 求解二次方程 二次方程 ax2 + bx + c = 0(a ≠ 0) 的解可由二次公式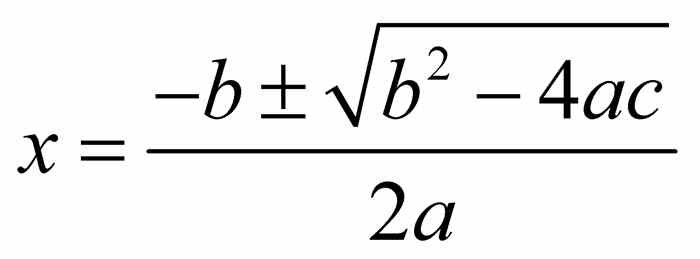 给出.对该公式的证明需要使用配方法.它包含几步代数变换,如下文中二次多项式 6 x2 + 28 x - 80 的例子所示.
给出.对该公式的证明需要使用配方法.它包含几步代数变换,如下文中二次多项式 6 x2 + 28 x - 80 的例子所示.
首先提取x2项的系数,则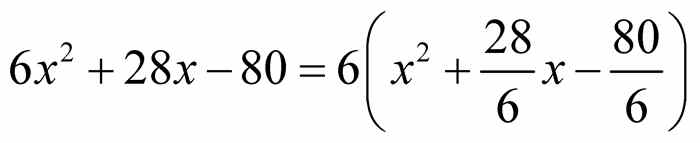 .注意
.注意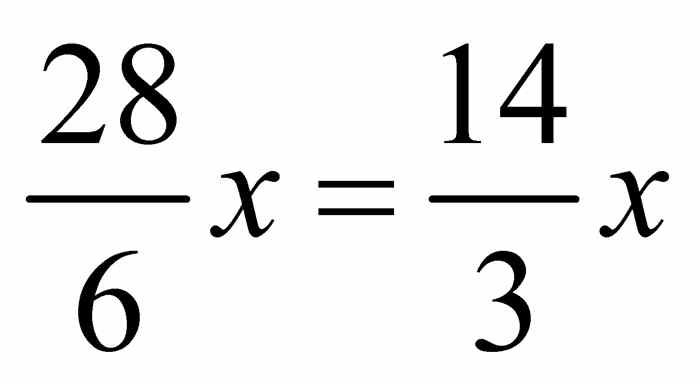 ,
,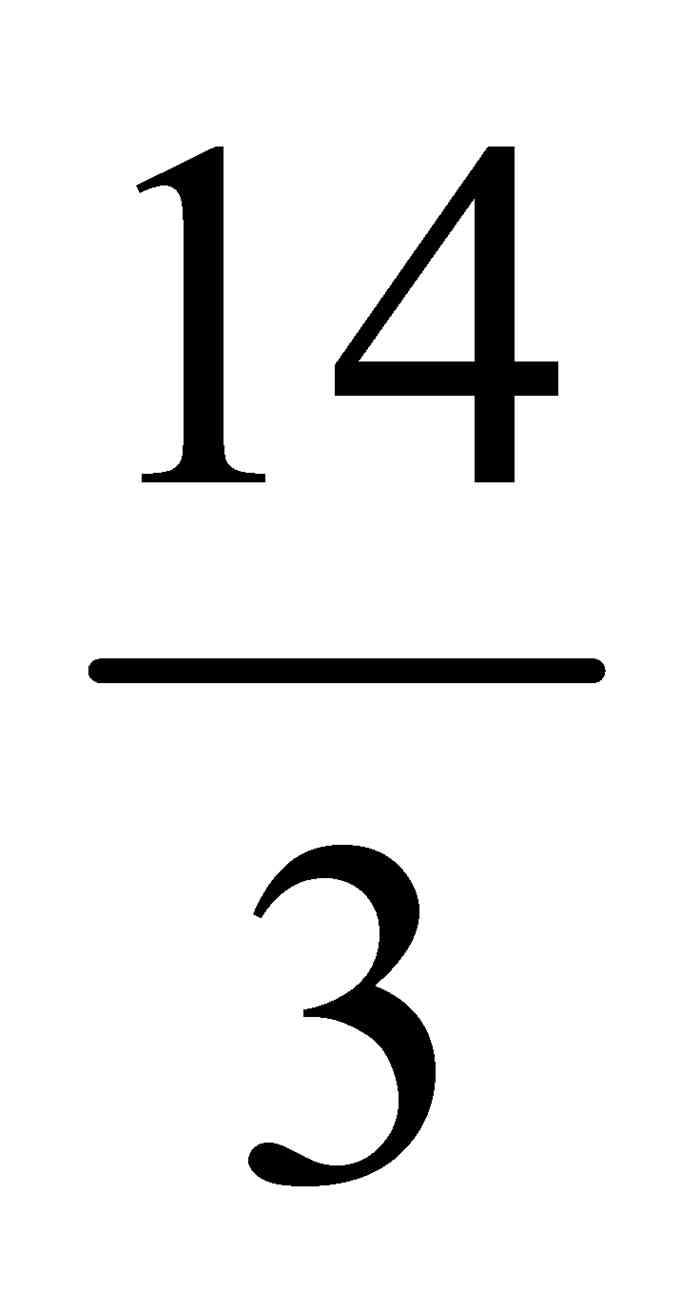 除以2得
除以2得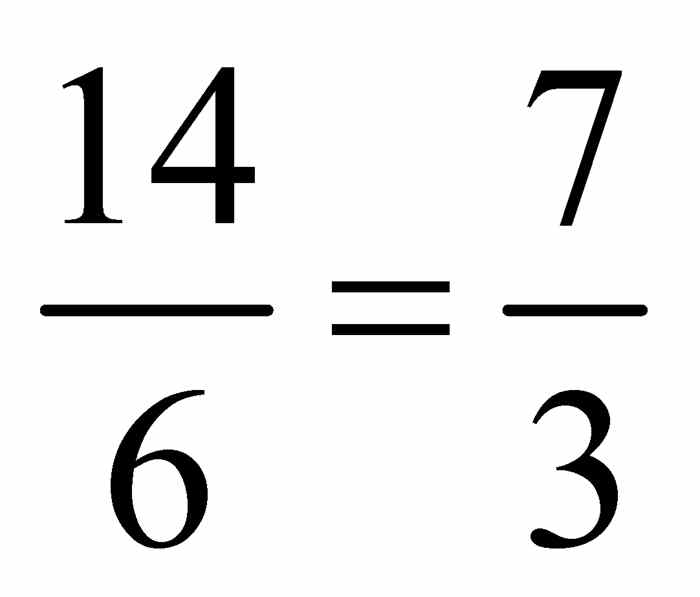 ,其平方为
,其平方为 .现在可将
.现在可将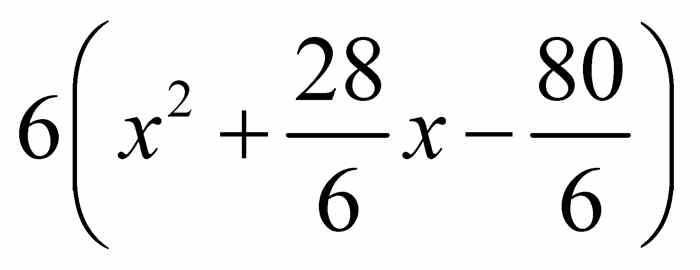 写作
写作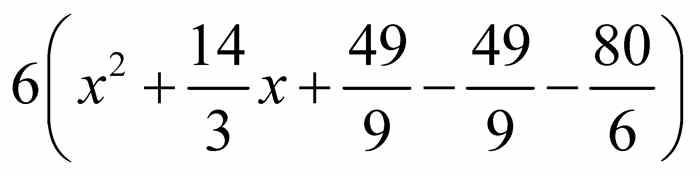 .重新结合得
.重新结合得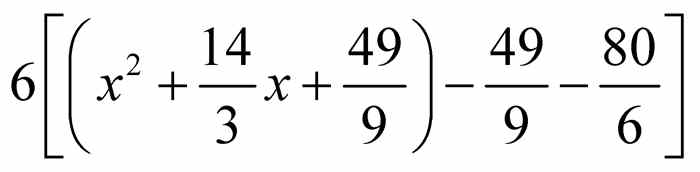 .因为
.因为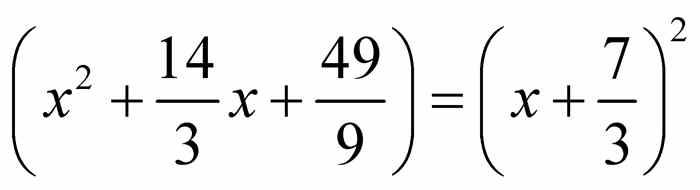 ,则有
,则有

将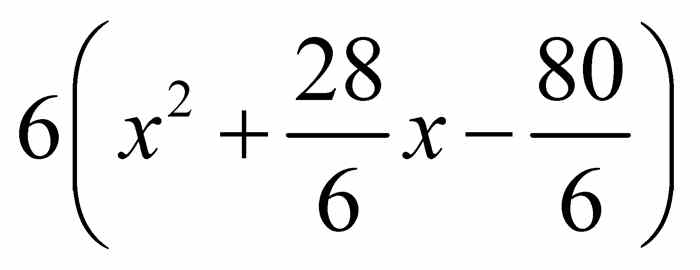 写成
写成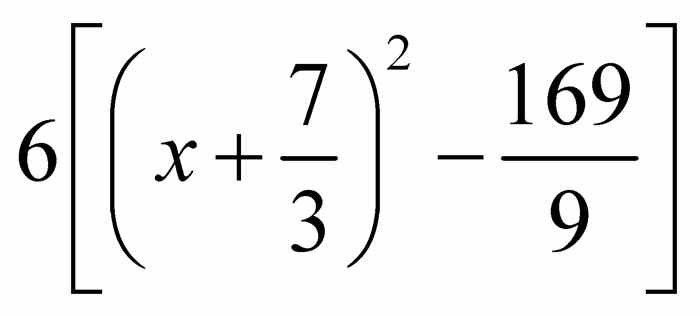 后,就完成了对二次多项式6 x2 + 28 x - 80的配方.现在就很容易求解 6 x2 + 28 x - 80 = 0中x的值了.将
后,就完成了对二次多项式6 x2 + 28 x - 80的配方.现在就很容易求解 6 x2 + 28 x - 80 = 0中x的值了.将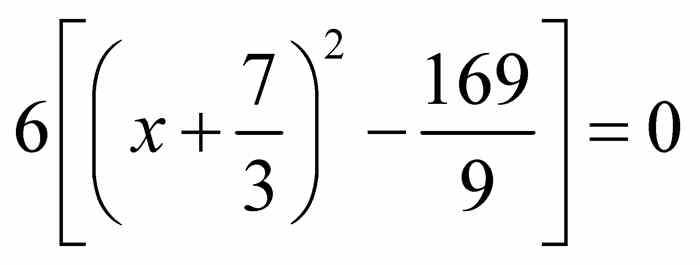 除以6,得到
除以6,得到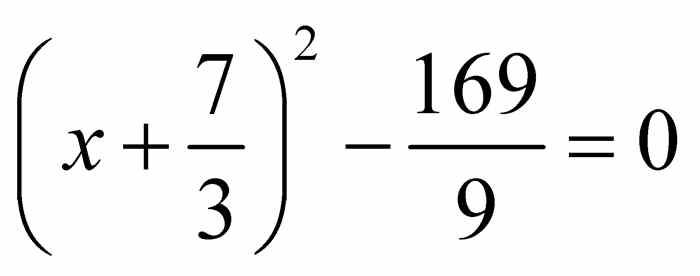 .由于
.由于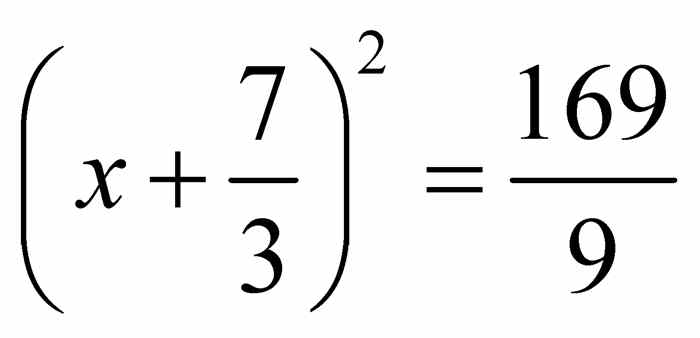 ,则有
,则有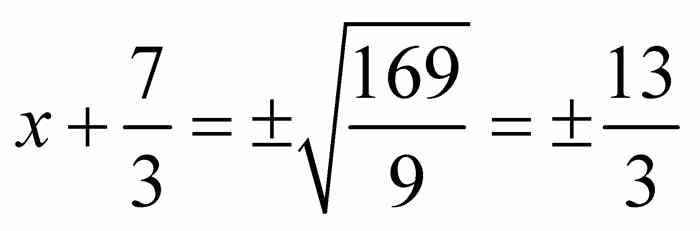 .因此有
.因此有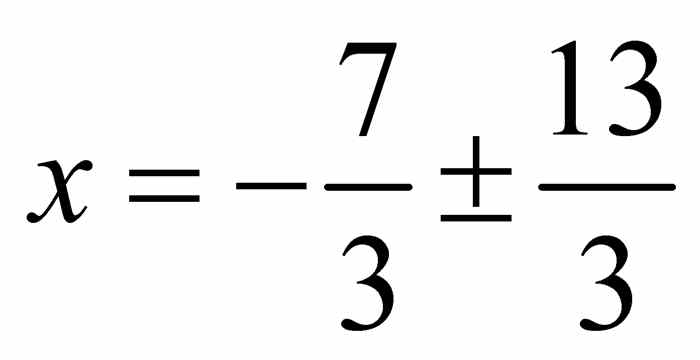 ,所以x = 2 或
,所以x = 2 或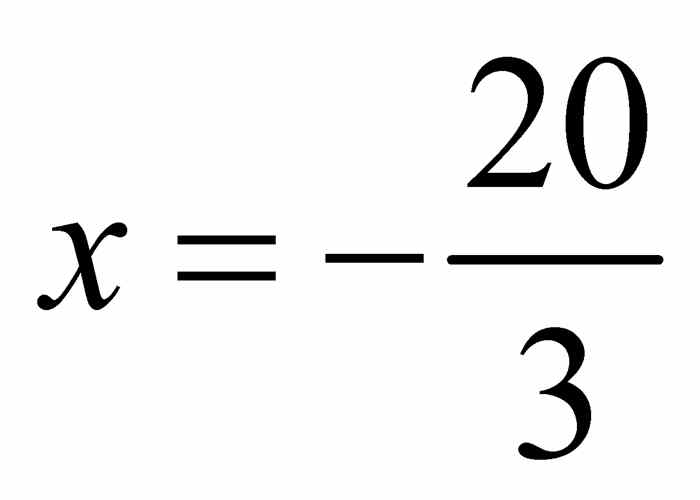 .
.
问题6 按照以上步骤完成4 x2 - 8 x - 12的配方.据此来求解4 x2 - 8 x - 12 = 0中x的值.
问题7 完成多项式 -5 x2 + 3 x + 4 的配方.然后据此求解 -5 x2 + 3 x + 4 = 0 中x的值.同样处理 -5 x2 + 3 x - 4 .【注意:方程 -5 x2 + 3 x - 4 的解需要求负数的平方根.在本文中我们不考虑复数,因此认为这样的方程无解.】
问题8 用配方法验证 ax2 + bx + c = 0 (a ≠ 0) 的解的二次公式 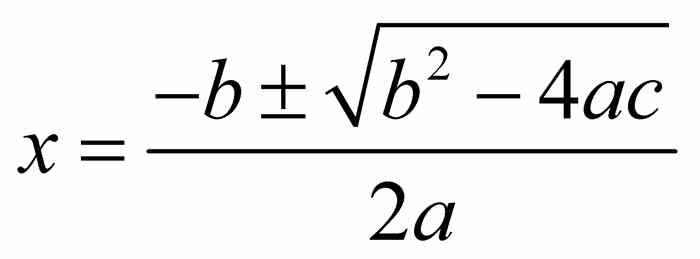 .当a = 0时,会出现什么情况?
.当a = 0时,会出现什么情况?
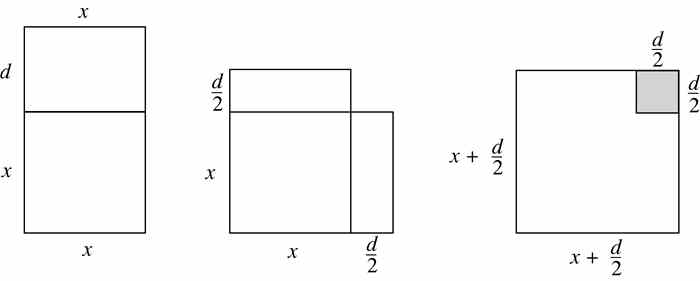
问题9 设x和d为任意正数.研究图1-14中的图形,讨论它们与配方法的联系.
在希腊建筑中到处都能看到基本几何图形.在构造建筑物时,希腊人把绳索系在钉子上,将其拉直并旋转,从而画出他们设计的直线和圆弧.希腊的几何学家将这种实践进行抽象,将其发展成对尺规作图的研究.这一研究收在欧几里得的《几何原本》里.让我们从卷1的两个基础作图看起.
从图2-4(a)开始.用直尺(没有刻度的标尺,不能测量长度)画出一条线段AB.将圆规的一只脚放在A点,另一只伸到B点,画出一个圆弧,如图所示.然后以B为中心,以同样的半径画另外一条圆弧.设C为两条弧的交点,这样就用尺规作出了等边三角形ABC.为什么角A、角B和角C均等于60°?(答案将在本章末问题1和问题2中得出.)现转向图2-4(b).设∠AOB为任意角.将圆规放在O点,画一条经过该角的圆弧,令C和D为圆弧与线段OA和OB的交点.将圆规的脚分别放在C和D点,画出两个半径相同的圆弧.设E是这两条弧的交点,则从O到E的线将∠AOB分成两部分.(见问题3.)这样用尺规将∠AOB进行了等分.
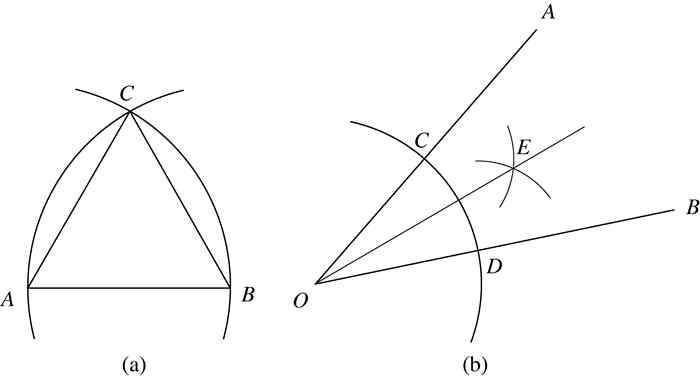
图 2-4
在第6卷中,欧几里得解释道:“一条线段被分割时,若整条线段与分割后的长线段的比等于长线段与短线段的比,则称这条线段以‘中外比’分割.”让我们从数学角度看一下这段话的意思.图2-5画出了一条被分成两部分的线段.其长度是a和b,且a ≥ b,则线段的总长是a + b.欧几里得认为如果a + b与a的比等于a和b的比,即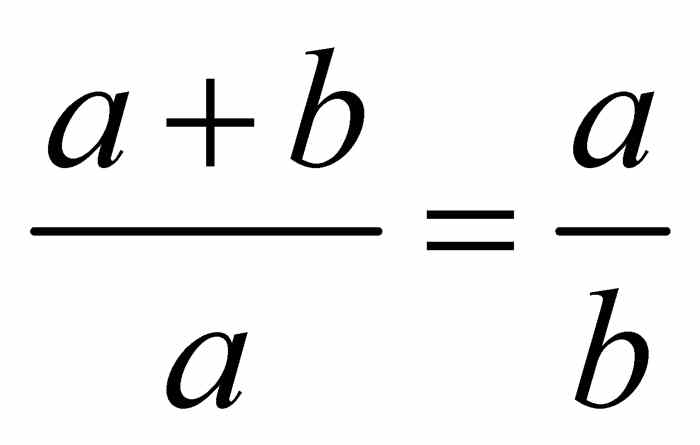 ,则该线段以“中外比”分割.注意此时
,则该线段以“中外比”分割.注意此时
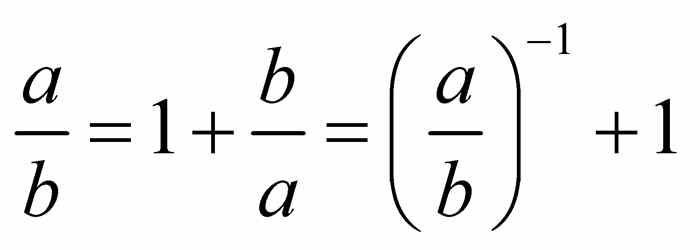
将此方程乘以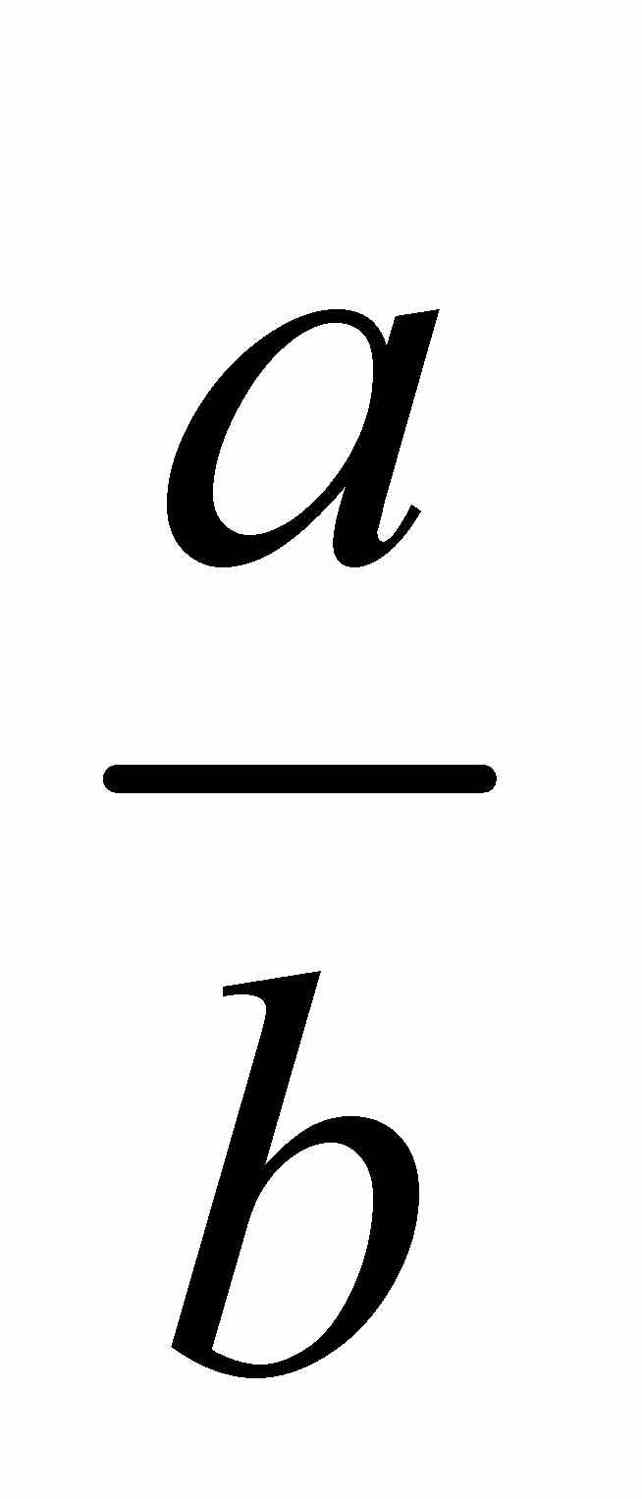 ,可以看出
,可以看出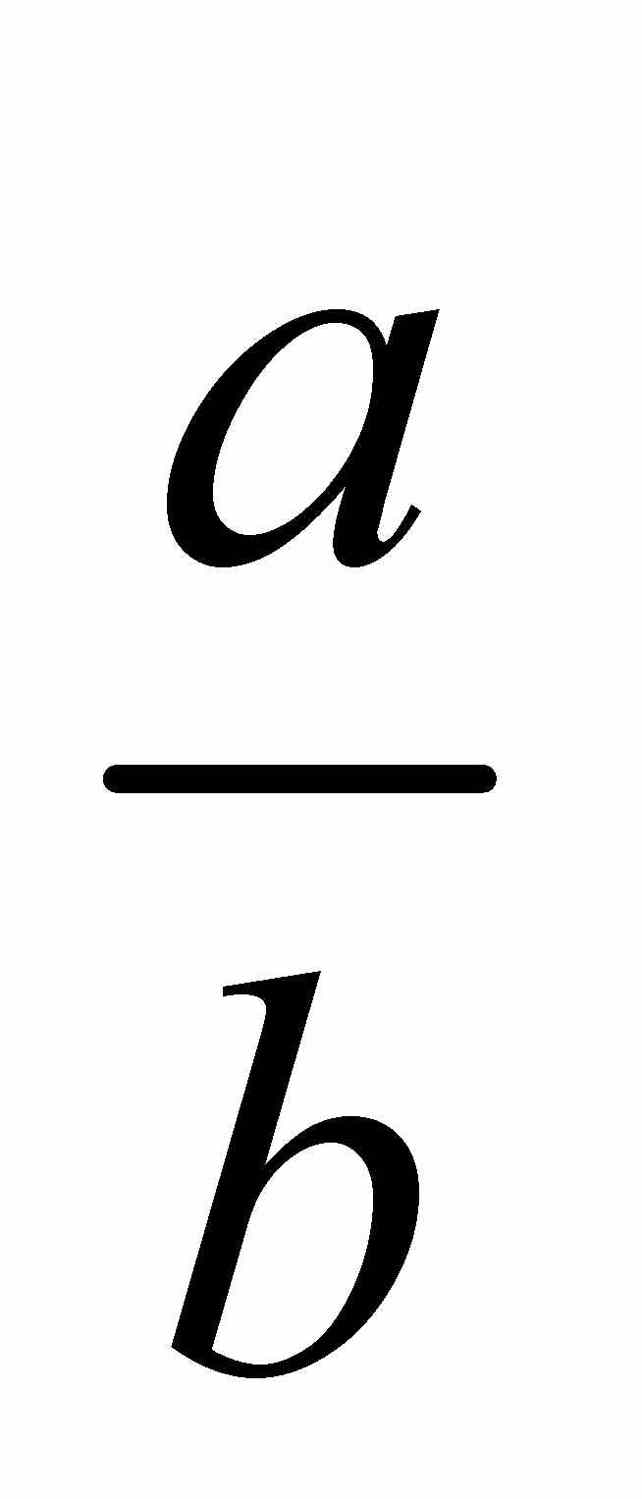 是多项式 x2 - x -1 的根.用二次公式可求得
是多项式 x2 - x -1 的根.用二次公式可求得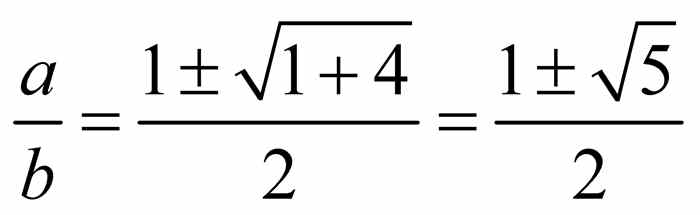 .由于
.由于 为正数,可得
为正数,可得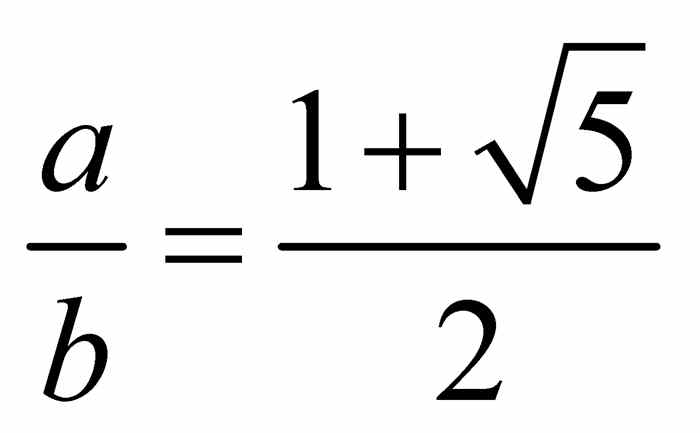 .
.

图 2-5
在现在的术语中,这样的分割是黄金分割,比率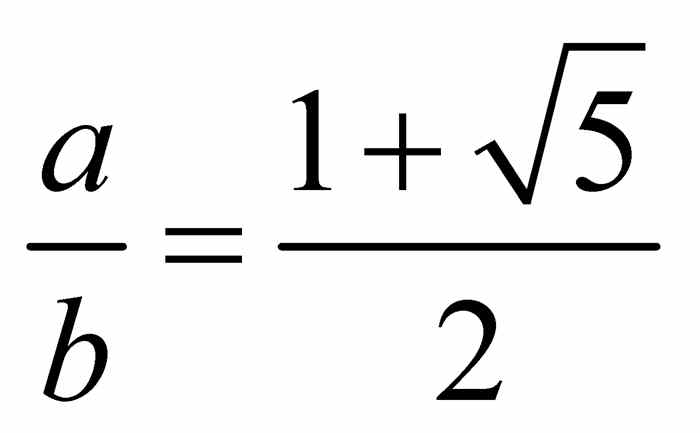 是黄金分割率.(这一比率也被称为神圣比率.)数学上习惯用希腊字母φ表示黄金分割率.一般人们声称这是对伟大的希腊雕塑家菲迪亚斯的纪念,据说他使用了黄金分割率.当然,这种比率本身确实引人注目,按照规定,它要求整体与较大部分的比等于较大部分与较小部分的比.
是黄金分割率.(这一比率也被称为神圣比率.)数学上习惯用希腊字母φ表示黄金分割率.一般人们声称这是对伟大的希腊雕塑家菲迪亚斯的纪念,据说他使用了黄金分割率.当然,这种比率本身确实引人注目,按照规定,它要求整体与较大部分的比等于较大部分与较小部分的比.
我们根据惯例,用小写希腊字母φ表示黄金分割率.则有
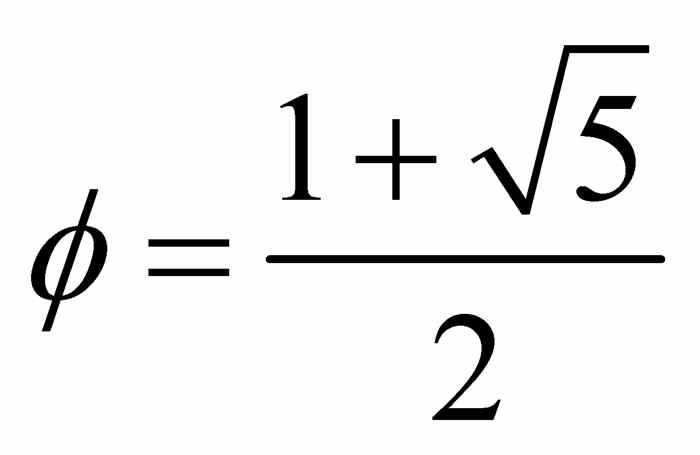
φ因为是多项式 x2 - x - 1的的根,则
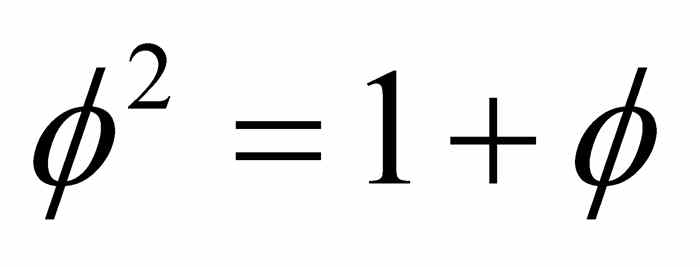 ,
,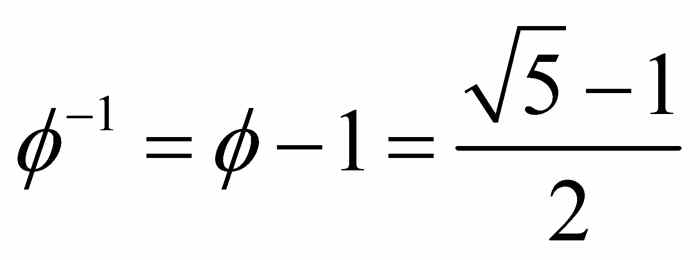
用计算器计算可得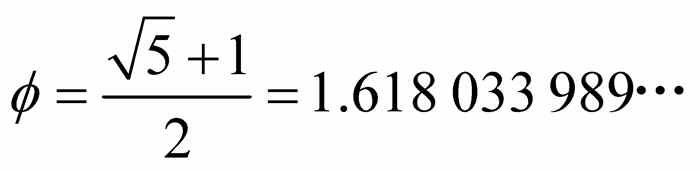 .
.
如果矩形的边长比率符合黄金分割率,则该矩形为黄金矩形.用尺规作出黄金矩形的方法如图2-6所示.设b为任意长度,以b为边长先画出一个正方形.可以通过平分180°角(给定一条直线及其上的一个点)得到需要的90°角,过程见图2-4(b)所示.现在找出正方形底边的中点,将圆规的脚放在该点上,将另一只脚沿虚线拉到正方形上面的一个角上.由毕达哥拉斯定理可知,该虚线的长度为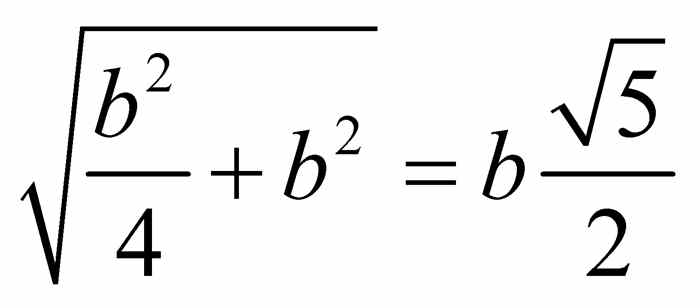 .向下旋转这一圆弧直到它与正方形底边的延长线相交.取该交点所确定的线段,完成图中所示的一个矩形.设a是该矩形的底边,注意
.向下旋转这一圆弧直到它与正方形底边的延长线相交.取该交点所确定的线段,完成图中所示的一个矩形.设a是该矩形的底边,注意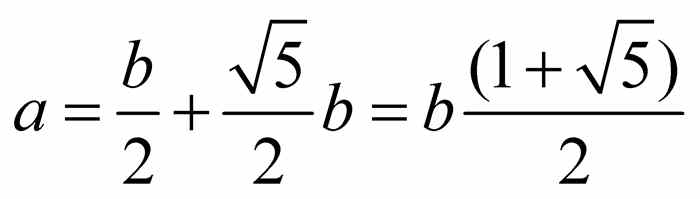 .因为
.因为
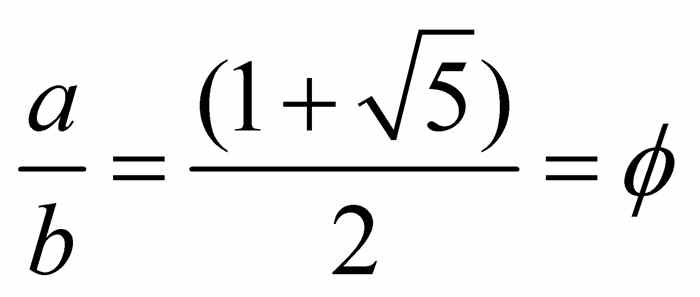
该矩形为黄金矩形.考虑黄金矩形的底边.正方形的右侧边将其分割成较长的线段b和较短的线段a-b.因为

则有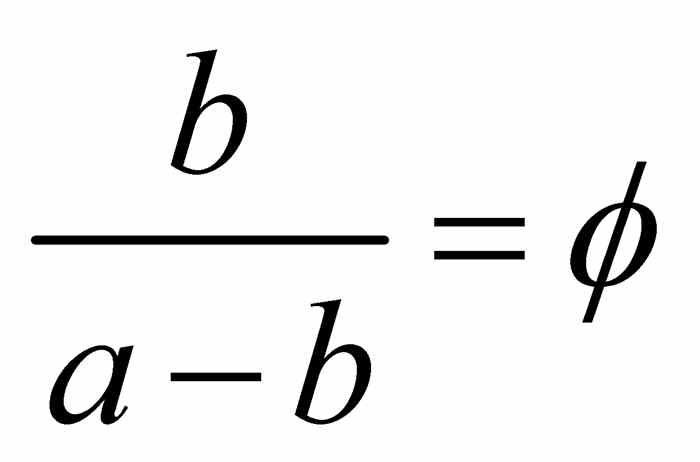 .这一分割是矩形底边的黄金分割.
.这一分割是矩形底边的黄金分割.
这一构造也告诉我们对任何线段而言在哪里“下刀”才能进行黄金分割.设AB为一条线段,将图2-6的构造添加到它身上,如图2-7所示.从黄金矩形底边的右端点D出发,画一条线,连接线段AB的右端点B.过点P构造一条它的平行线(如何构造平行线见问题6).这条平行线确定了线段上的C点.根据相似三角形的基本性质(见问题16及该问题的引言),有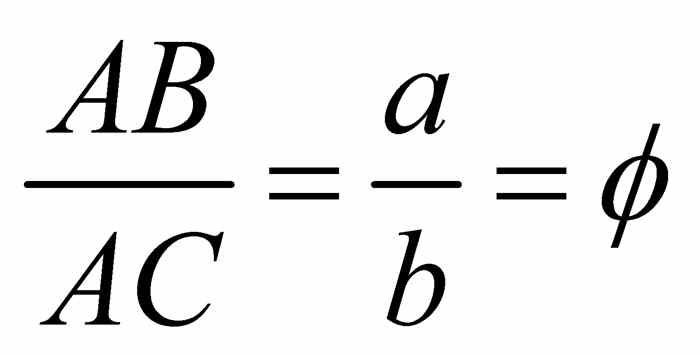 .因为
.因为 ,
,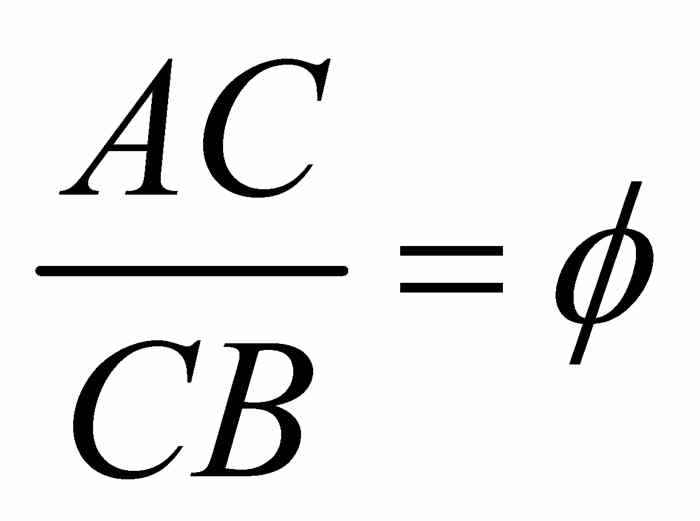 .因此
.因此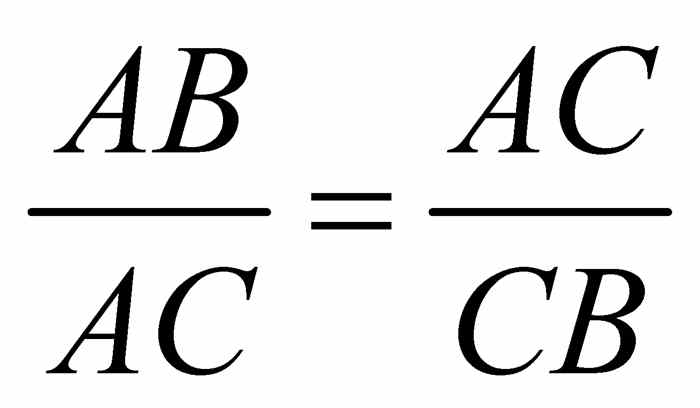 ,C处的分割是黄金分割.
,C处的分割是黄金分割.
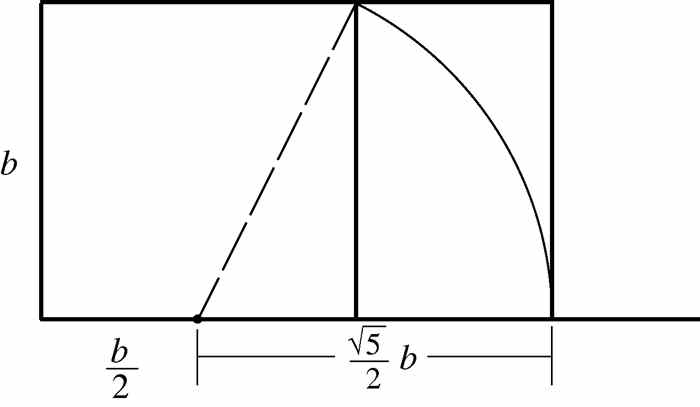
图 2-6
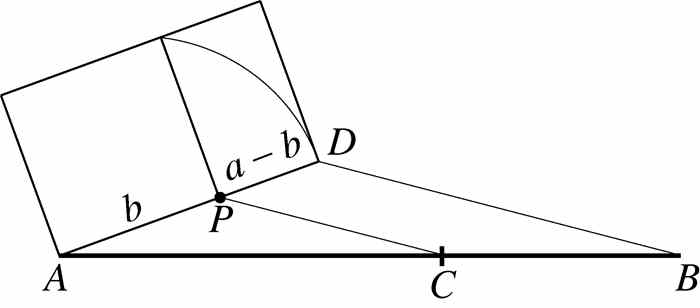
图 2-7
以上提出的这些所有构造均可以只通过一个用来画圆弧的圆规(这是对钉子和绳子作用的抽象)和一把连接端点的直尺(这是模仿两个钉子间拉长的那条绳子)来实现.任何尺规作图都必须满足只能使用上述两种工具的要求.
平面内的一个多边形包含多个点,这些点通过线段进行连接,从而形成一个闭环.图2-8(a)给出了一个典型的例子.称点 V1 、 V2 、 V3 等为顶点,连接它们的线段为边.图2-8(a)中的多边形有10个顶点,则被称为十边形.如果一个多边形有n个顶点(或n条边),则为n边形.如果所有的边长都相同,所有的内角 α1 、 α2 、 α3 等均相等,则该多边形是正多边形.图2-8(b)展示了一个正七边形.它是通过在一个圆周上等距离分布点 V1,V2,…,V7 得到的.因为圆被等分成7份,则每个圆心角的度数都是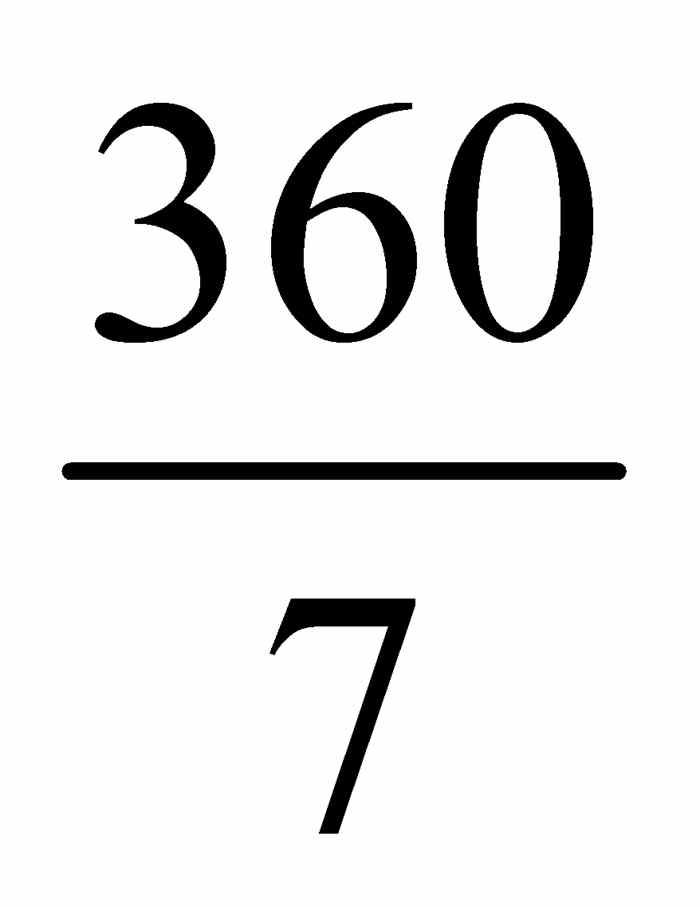 .
.
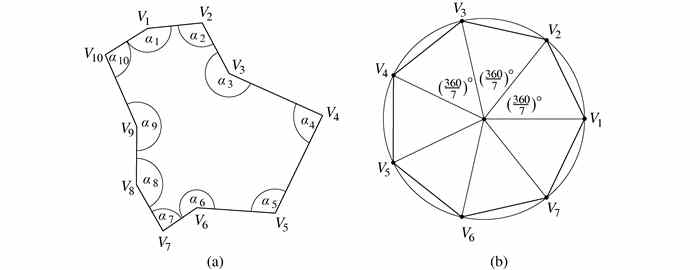
图 2-8
我们回头来看能用尺规构成哪些正多边形.图2-4(a)告诉我们如何构造等边三角形.构造黄金矩形是从构造正方形开始的.因此,正三角形和正四边形都能用尺规构造.构造正n边形最直接的方法是构造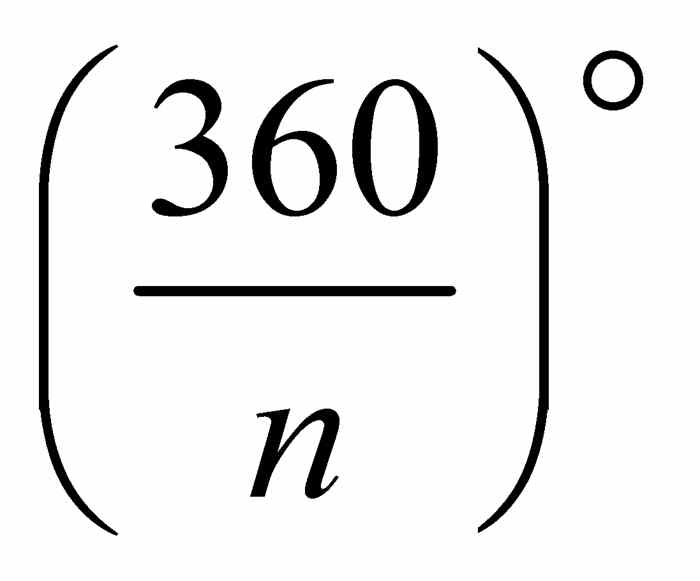 角.如果能构造出这个角,就能在一个圆上标出n个等距离分布的点.用线段连接圆上相邻的点就能画出正n边形.例如,构造等边三角形时构造了60°的角,连续划分出60°角,得到点 H1、 H2 、 H3 、 H4 、 H5 、 H6 ,如图2-9所示,这样就构造出正六边形,即六方形.平分90°角得到45°角,重复划分45°角可确定图2-9中的点 O1,O2,…,O8 ,因此构造出正八边形.
角.如果能构造出这个角,就能在一个圆上标出n个等距离分布的点.用线段连接圆上相邻的点就能画出正n边形.例如,构造等边三角形时构造了60°的角,连续划分出60°角,得到点 H1、 H2 、 H3 、 H4 、 H5 、 H6 ,如图2-9所示,这样就构造出正六边形,即六方形.平分90°角得到45°角,重复划分45°角可确定图2-9中的点 O1,O2,…,O8 ,因此构造出正八边形.
还能构造正五边形.首先如图2-6那样构造黄金矩形.在图2-10中,分别以A和B为圆心,以b为半径画两条圆弧.点C为两条弧的交点.可以证明∠CAB = 72°.因此,可以构造出72°角.5次标出这一角度,得到图2-9中的 P1 、 P2 、 P3 、 P4 、 P5 .因为 5×72°= 360°,这样就完成了正五边形的构造.
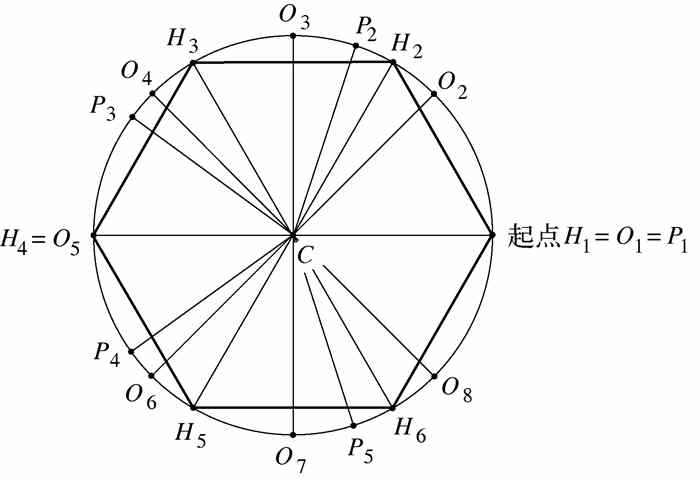
图 2-9
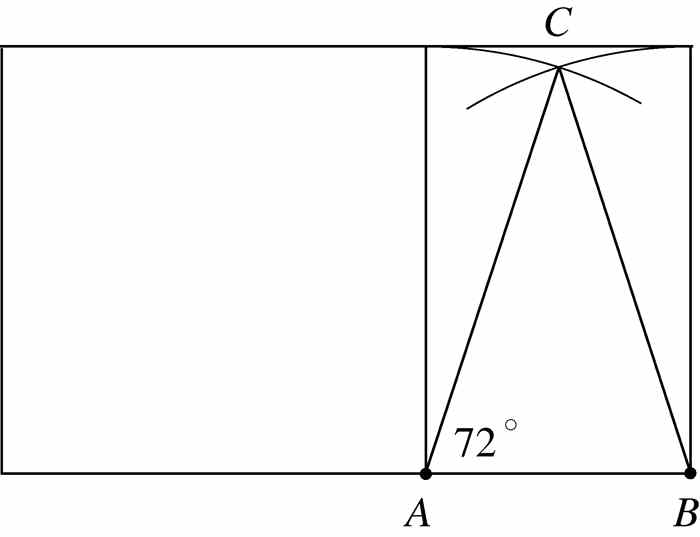
图 2-10
不过我们怎么知道∠CAB = 72°?详细答案有些复杂,但主要的原因如下.首先看图2-11(a)中位于中心的正五边形.(不能假设该五边形能被构造,而且它也不是被构造出来的,否则说明你正在假设需要进行证明的结论成立.)点O是五边形的5个顶点所在的圆的圆心.因为 5 γ = 360°,内角γ等于72.根据等腰三角形的基本性质,β = 45°,则有2 β = 108°.现在用该五边形完成一个五角星.转到图2-11(b),像图中那样标出点A、B、C和D.注意∠CAB=72.现在到了最难的部分,即需要证明以DA为一条边的正方形沿线段AB拉长后得到的矩形是黄金矩形.讨论2.2详细描述了欧几里得在他的《几何原本》中是如何做到的.剩下的就简单了.线段DA和AC长度相等表明图2-10和图2-11(b)中的三角形ABC是用同样的方式获得的.因此,图2-10中的∠CAB确实等于72.
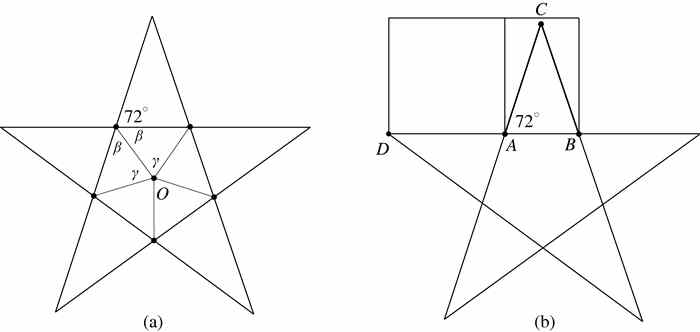
图 2-11
现在我们已看到边数为3、4、5、6和8的正多边形都能用尺规构造出来.这一事实提出了一个有趣也非常难的问题:正多边形的边数,即正整数n为何值时,能用尺规进行构造?直到19世纪,数学家们才向着答案的方向迈出了一大步.只有当这一几何问题转化为高等抽象代数问题(尤其是转化成系数为有理数的多项式的根的问题)之后,它才被彻底解决.例如,该方法指出,边数从3到1002的正多边形中,换句话说,前1000个正多边形中,那些边数为如下所示数值的可以被构造出来,而其他的都不能.
3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 30, 32, 34, 40, 48, 51, 60, 64, 68, 80, 85, 96, 102, 120, 128, 136, 160, 170, 192, 204, 240, 255, 256, 257, 272, 320, 340, 384, 408, 480, 510, 512, 514, 544, 640, 680, 768, 771, 816, 960
数一下就知道,1000个正多边形中,只有52个是能被构造出来的.因为7不在其中,则图2-8(b)中的正七边形不能被构造.因为9不在其中,则正九边形也不能被构造.注意这张表中,数字的间隔很大.这些及其他相关的事实远远超出了本文的目标和范围,不过在讨论2.3中还会略有提及.
正如我们已注意到的,希腊的建筑实践明确地影响了希腊几何学的发展方向.反之,希腊几何学,如三角形、半圆形、圆,也在其伟大建筑中得到了表达.不过影响有多深?在建筑设计或施工时,希腊建筑师试图坚持精确的数学比例或严格的几何关系吗?人们一般用帕提农神庙作为例子,说明他们确实是这样做的.证据如图2-12中的框图所示.帕提农神庙正面的许多黄金矩形能告诉我们希腊人将黄金矩形作为一个模板吗?他们是如何选择矩形和正方形的,而这种选择的相关性如何?它们的位置如何确定?精确度又如何呢?这是证明他们有意使用黄金矩形来完成设计的有力证据吗?还是黄金矩形只是人们事后强加到建筑立面的?不管是作为数字还是通过构造得到的黄金分割率都是非常准确的.具体而言,它不等于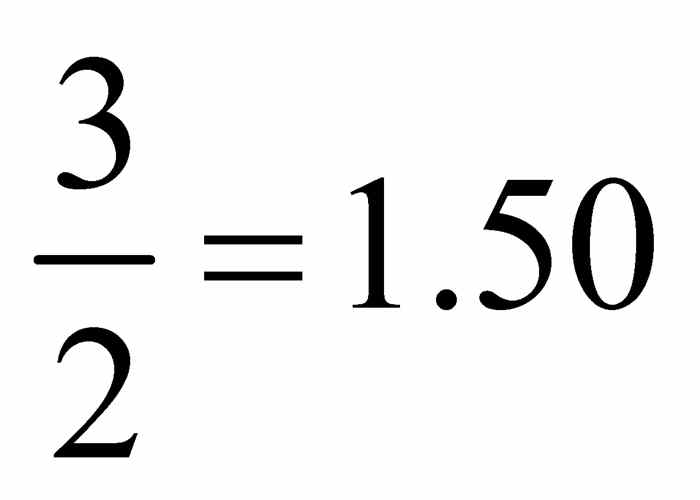 或
或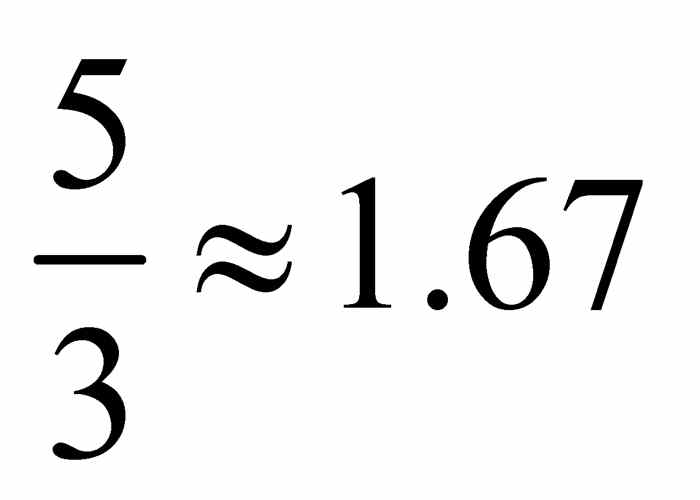 ,也不等于
,也不等于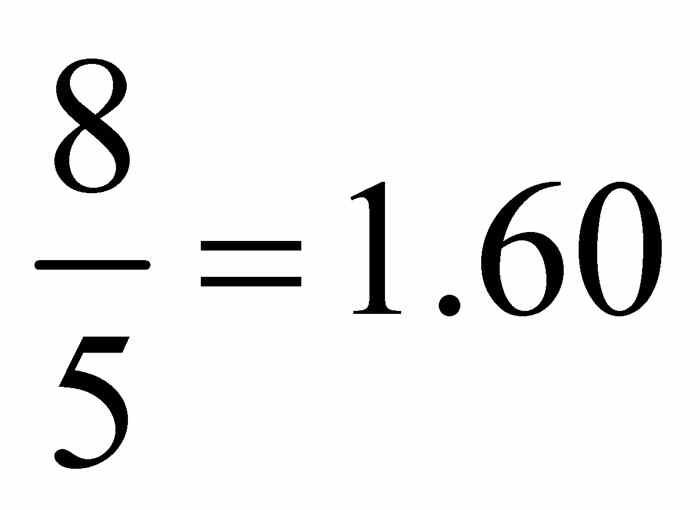 .并没有决定性的证据证明希腊建筑人员在建筑设计和实施时遵循了精确的几何关系.实际上,图2-2中埃皮达鲁斯圆形神庙的平面图表明他们没有这样做.注意,这张平面图的特点是14根柱子排成的内圆和26根柱子排成的外圆.标出这些圆柱位置的圆的圆心分别是十四边形和二十六边形的顶点.因为14和26均未出现在上文提到的边数列表中,因此我们知道不可能构造出正十四边形或正二十六边形.如果说精确的施工对希腊人而言很重要,在布置这些圆柱时,他们难道不应该使用正十二边形和正二十四边形吗?他们知道如何用钉子和绳子精确构造这些多边形,只要先作出正六边形,再使顶点数加倍两次就可以了.
.并没有决定性的证据证明希腊建筑人员在建筑设计和实施时遵循了精确的几何关系.实际上,图2-2中埃皮达鲁斯圆形神庙的平面图表明他们没有这样做.注意,这张平面图的特点是14根柱子排成的内圆和26根柱子排成的外圆.标出这些圆柱位置的圆的圆心分别是十四边形和二十六边形的顶点.因为14和26均未出现在上文提到的边数列表中,因此我们知道不可能构造出正十四边形或正二十六边形.如果说精确的施工对希腊人而言很重要,在布置这些圆柱时,他们难道不应该使用正十二边形和正二十四边形吗?他们知道如何用钉子和绳子精确构造这些多边形,只要先作出正六边形,再使顶点数加倍两次就可以了.

图2-12 使用黄金比率的帕提农神庙,Padfield摄
15世纪,文艺复兴时期的建筑师提出并开始使用比例数学系统.他们依照固定的数字比例,整理了建筑构件的各种尺寸,包括柱子、支撑柱子的柱础以及柱子所支撑部件的粗细和长度.5.2节及讨论5.1中会提到这部分内容.